［文系型］ 2020年2月1日　大問[1] (1)

与えられた関数の式を、場合分けによって絶対値を外す、さらに平方完成することにより、2つの変域つきグラフ（放物線）を1つの平面に表すことでグラフを用いて見通しを立てるとよいでしょう。また、それぞれの放物線と傾きmの直線の共有点のx座標は、文字定数を含む方程式を解くスキルが要求されます（本問は、x=0で共有点をもつことが式からもグラフからも明確）。「3つの共有点をもつ」という条件を、「それぞれの放物線と、その変域内で共有点を1つずつもつ」という条件に落とし込む条件の解釈力が要求されます。

［文系型］ 2020年2月2日 　大問[1] (1)

三角比の定義を用いて三角比の値を求めるといった基本に忠実な静かなオープニングから、三角形の内心の性質、つまり角の二等分線の性質に注目し、求めたい△ABCと先に注目したsin∠OBDが△ABC=2sin∠OBDであることから、三角関数の倍角の公式に結びつけることができるかが問われています。図形と計量（数学Ⅰ）、図形の性質（数学A）、三角関数（数学Ⅱ）といった複数の分野の知識を融合して課題を解決するスキルが必要です。さらに、求めた△ABCに注目をしていれば、次のAHは三角比の定義で求められます。そのAHが、三角形ABCにおいて辺BCを底辺としたときの高さであることから、三角形の面積の利用が頭に浮かぶこと、さらにその面積は、三角形の内接円の半径と三角形の周の長さで表されるといった典型的な解決の手法が頭に浮かぶこと、その周の長さは、求めるCDの長さをxとおくことで求められること、つまり与えられた情報と今まで求めたもの、最終的に求めたいものといった点と点が、意味を理解した演習によって線でつながることで、問題解決に至ります。

［文系型］ 2020年2月1日　大問[1] (2)

確率を解決する視点として最も大切なものの1つである排反な事象に分けることが求められる問題です。「1が出る」という事象Bを考えるとき、1の枚数に注目をし、1が1枚のみという事象と、1が2枚とも出るという排反な事象に分け、さらに1が1枚のみのときを、赤の1のみ、白の1のみ、という排反な事象に分けることができます。このそれぞれにおいて、さらに白が1枚のみ出るという事象Aが同時に起こるときはどんなときかを考えることで、ダブルカウントや抜け漏れを防ぐことができます。一方で、事象Aから先に考え、その1枚が1（残りは赤4枚から2枚）か、1以外（残りは赤の1と、それ以外の1枚）か、という排反な事象に分け考えることもできます。ただし、次に「赤の1が取り出される」という事象Cを条件付き確率で扱うため、そのタイミングで、前者の「残りは赤4枚から2枚」という事象をさらに「赤の1とそれ以外」の場合（3通り）と、「赤の2～4から2枚」（3通り）という排反な事象に分ける必要があります。事象Cは問題文で可視化されているので、見通しを明るくし、適した方法を選択するスキルがあるとよりスムーズに問題を解くことができるようになるでしょう。

［文系型］ 2020年2月2日　大問[1](2)

試行ごとに状況がリセットされる反復試行の確率においては、場合の数の純粋なスキル、つまり何が何回どこで起こり、それは何通りなのか、が問われます。さらに、この問題のように個数が異なるものが含まれる場合は、それが起こる確率が異なりますので、分けて考える必要があります。「すべて一致する」場合は、何回目でそれが起こるのかは考える必要がありません。冒頭の問題がこのように「すべて同じ」の場合、次の問題において「2つのみ一致、1つは異なる」のような「異なる場合を扱う」に、一致する2つは3回中どこの2回で起こったのかを決める3C2の計算が抜けてしまう傾向にあります。反復試行の公式をまる暗記している人は太刀打ちできないでしょう。最後には三角形の成立条件を考える必要がありますが、辺の長さとして扱う3つの数字が可視化されているので、もっとも大きい数字に注目して、（最長辺の長さ）<（他の2辺の長さの和）にあてはまるか確かめる方法を知っていると素早く処理できます。

［文系型］ 2020年2月1日 　大問[2] (1)

領域内の点の座標を用いた最大・最小の問題で、典型的な問題です。領域の境界を表す方程式を連立して境界の端点の座標を求める、値を求めたい式をkとおき、kの図形的な意味を考えてその最大、最小を求める、領域を図示した上で、直線の傾きに注目、円と直線が接するときの条件、点と直線の距離、2円が接するときの接点の座標など、条件を満たす場面とそれを解決する手法をその場に応じて適切に選択できるスキル、さらにそれを着実に遂行する計算スキルが求められています。

［文系型］ 2020 年2月2日 　大問[2] (1)

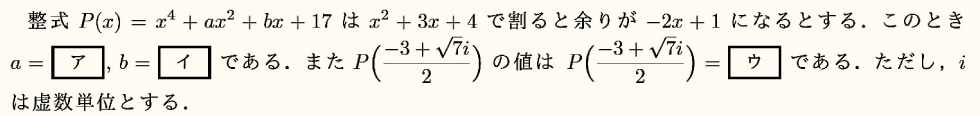
整式の割り算の結果が示され、そこから除法の原理を用いて、実際に割り算することなく割られる式を求めることにより、その式に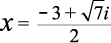を代入した値を求める問題です。実際に値を代入するパワープレイは全く求められておらず、割られる式を求める際に同時にわかる商と、除法の原理を用いて等式を立て、さらに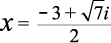が商を0にする値であることから、余りの部分に含まれるxに値を代入すれば終了します。入試においては典型的な問題ですが、除法の原理を用いて式の値を工夫して求める経験が問われている、ある意味シビアな問題です。

［文系型］ 2020 年2月1日 　大問[2] (2)

空間ベクトルにおいて、(i)では、成分表示された2つのベクトルの内積、2ベクトルが垂直、単位ベクトル、(ii)においては、共面条件の理解、(iii)においては、成分表示されたベクトルの大きさ、複2次式、2次関数の最小が問われています。この分野における基本的な知識・技能とその利用ができる状態により、完答が期待できます。さらに、(i)においては外積、(ii)においては(i)の結果と平面の方程式の知識を用いることで、よりスムーズに解くことか可能です。

［文系型］ 2020 年2月2日 　大問[2] (2)

等差数列とその一般項、等比数列とその一般項、等差数列の和、等比数列の和が問われる問題で、問われる知識・技能だけ見ると教科書レベルなのですが、この問題の特徴は、与えられる初項a、公差d、公比rがすべて文字定数であることです。条件によって立式し、それを用いることで文字定数の値は徐々に明らかになっていきますが、文字定数を用いて立式し、文字定数のまま条件を処理する経験を積むことが必要で、それが乏しいと、持っている知識・技能がまったく発揮されずに終わる可能性がある問題です。

［文系型］ 2020 年2月1日 　大問[3]

３次関数において、(1)では、極値とそれをとるxの値から元の式を求め、もう1つの極値を求める問題、(2)では組立除法による因数分解と、2次方程式の解と係数の関係、対称式の知識を用いた求値、(3)では(2)の値を用いて3次関数のグラフとx軸で囲まれた部分の面積を求める問題です。(3)においてはグラフとx軸の交点の大小関係およびグラフとx軸の上下関係に注目する必要がありますが、(2)も含めて誤認が起こらないように配慮されています。完答のためには極値や面積の計算において、長きにわたる計算を着実に実行する力が求められます。

［文系型］ 2020 年2月2日 　大問[3]

３次関数のグラフの接線の傾きが最小になるときのxを、微分した式と2次関数の最小の知識を用いて求め、(1)においてはそのx座標-aを、接点のx座標が文字定数で与えられた接線の方程式を求める問題として解いていきます。接線の式をy=ax+bの形に整理することがマストで、この問題に関しては美麗な式になります。(2)では、文字定数を含む式の因数分解によって極値をとるx座標を求め、その大小の判断、および極値を文字定数aを用いて表し、極値が0という条件を用いてaの値を求める問題です。極値をaを用いて表すパートでは、式を展開するのではなくその後を見据えて共通因数に着目して因数分解していくことが必要です。(3)は、3次関数のグラフと接線および直線で囲まれた部分の面積を求める問題です。(2)のaの値と、(1)の接点のx座標が-aであることを強く意識すること、さらに問題の設定で「接線の傾きが最小のとき」をグラフ的にとらえることで、上下関係も含めてグラフを迷いなく書くことができます。またグラフの上下が直線の場合の面積は、三角形の面積の公式などを利用して工夫して求めることが可能です。

［理系型］の試験範囲には数学Ⅲが入りますが、微分・積分の基本的なスキルと、それを使って問題を解決する標準的な場面の経験を積むことで、合格に必要な答案を作り上げることができます。