






当初は記述式の問題が導入される予定でしたが、それは見送られ、すべてマーク式になりました。配点や問題構成は、センター試験から大きな変化はありません。ただし、数学I・Aの試験時間は60分から70分に。「考察する時間」が加えられた形です。

大学入学共通テストでは、「正しい答えが出せるかどうか」に加えて、「解答に至るまでのプロセスを理解しているかどうか」を問う問題が出題されます。そのため、暗記した定義や定理を使って計算する力だけでなく、一つひとつの定義や定理を深く理解して、自ら使いこなすレベルの力が必要になってきます。たとえば試行試験では、正弦定理の証明の穴埋め問題が出題されています。ここでは、「正弦定理を知っているか」ではなく「正弦定理を理解しているか」が問われているわけです。

試行試験では、会話文で構成される問題や、複数の資料やデータが盛り込まれた問題も出題されています。ここでは、文章を読解する力や、身近な問題を数学的に捉えて解決する力、複数の情報をまとめたうえで解法を導き出す力などが問われています。全体の情報量が多いので、時間的には少々厳しい試験になるかもしれません。

問題を解くために必要な知識は、教科書の範囲を超えるものではありません。ただし、「教科書レベル」という言葉は「軽んじて良い」という意味ではありません。前述の通り、問われるのは知識量ではなく運用力。知っていても使えなければ意味がありません。その点を肝に銘じ、幅広い問題に取り組んで運用力を鍛えましょう。
大学入学共通テストには過去問は存在しません。よって、試行試験とその解答・解説、さらにオリジナル問題がセットになったものを入手し、チャレンジしましょう。時間を測る必要はありません。まずはどのような問題設定なのか、じっくり読み、問題に取り組んでください。
大問1問を解き終わるたびに、全体のプロセスを振り返りましょう。解答・解説を参考にするときは、じっくり丁寧に読むことも大切ですが、あえて時間に制限を設けて読み解くことをおすすめします。それは、出題者の真意を素早く読解する練習につながります。
解答・解説を読んだ後に改めて問題文を読めば、問題文で提示されていることから直接的にできることは何か、問題をどのように分解できるのか、分解されたそれぞれはどのような手法で解決できるのか、それらをどのような順番で運用すれば解決に至るのか、などが分かります。そうすることで、問題の構造を把握し、論理展開の整理を行い、プロセスの全体像を把握し、体系化をすることが可能となります。その整理された結果は、他の問題を解くときにダイレクトに転用できる場合もあるでしょう。構造を把握する力は、未知なる問題にも転用できる汎用的なスキルです。
次に、センター試験の過去問に取り組みましょう。すでに取り組んでいるという人も、上記の学習で培った観点をもって、改めて問題に向き合ってください。センター試験は、「資質・能力をマーク式で見る」というコンセプトのもと、長い年月をかけて深く練られた問題になっています。行間を読み、自分で流れを推測し、補足しながら解き進めるという点は、大学入学共通テストにも踏襲されます。センター試験の過去問を通じて、さらに学びを深めましょう。
仕上げとして、大学入学共通テストの対策問題集で実践力を高めましょう。もちろんその際も、解き終わった後の振り返りが大切です。時間内に収めることを意識するのは、復習が終わって再度取り組むときでOKです。
大学入学共通テスト対策で培った力、すなわち、問題や設問で与えられた情報を整理し、分解し、意図を理解し、それを解答として表現する力は、大学個別試験の過去問にも生かすことができます。逆に、個別試験対策で培った分析力・構築力は、大学入学共通テスト対策にもつながります。ぜひ意識して学習に取り組んでください。
センター試験と比べ、より知識の深い理解と、知識を活用する力(思考力・判断力・表現力)が問われることが予想されます。平成30年に行われた「第2回試行試験」から、その傾向を見ていきましょう。

(*)は「正弦定理」です。この問題は、正弦定理を知っているか(暗記しているか)を問うものではありません。あえて定理を提示することで、上記の問題文の後に提示される「(*)が成り立つ理由」、いわゆる「証明」のプロセスを読み、その流れや意図を理解できるか、といった「読解力」「思考力」にフォーカスを当てています。また、その証明プロセスを知っている人に対しては、与えられたプロセスと自分の知っているプロセスから一致点と相違点を見分ける力、つまり「判断力」が問われています。このほか、解決プロセスを振り返り、得られた結果を意味づけ、それを活用できることも重要なスキルとなります。
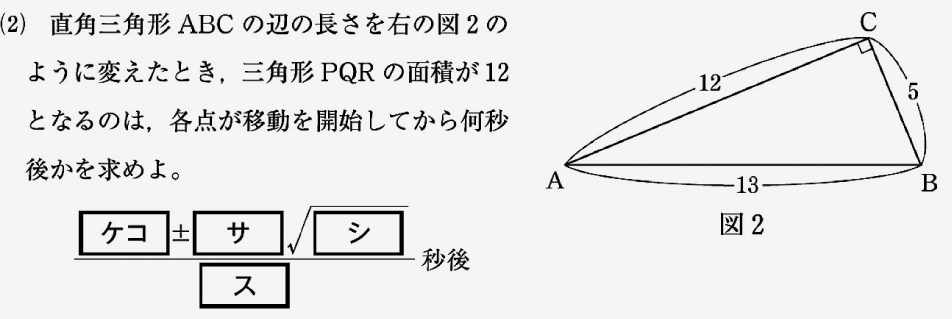
この問題の条件は「△PQRの面積が12」です。△ABCの面積は30であることがわかるので、「△ABCから△PQRを除いた残りの3つの三角形の面積の和は18」と解釈できます。これによって、その3つの三角形は、この問題の1つ前の問題である(1)(iii)で話題になった三角形であることに気づきます。(1)の図を(2)のように変化させたとき、(1)では与えられているが(2)では自分で求める必要があるものが存在することを判断しつつ、(1)(iii)のプロセスを転用できる力、および立式や計算を確実に遂行する力が問われます。
「話し合い」やそこで行われる「試行錯誤」によって見えてくることを、まるでその場に参加しているがごとく読み取り、個別の事象またはそれらを体系化したものを元に、正しいもの・誤っているものを選ぶ、といった、「実際の学びの場を想定した問題」も出題が予想されています。


現実では、試行錯誤のすべてに意味があるわけではありませんが、数学の試験において、会話によってわざわざ与えられた数値的な情報には何かしらの意味がある、と考えるのが自然です。また,上の問題では,いくつかの試行錯誤の結果から、一般化はできないまでも他のケースにあてはめて考えることができる、という力も見られています。さらに,その会話の内容には「仮説」が含まれる場合もあります。

たぶんそうだろう、という「感覚」に基づいて会話を進めることは、日常でも起こりえることです。その感覚に基づく仮説が正しいかどうかを、数学の力で解き明かしていくことが、数学を学ぶ意義です。上記の問題は、そのプロセスおよび検証を題材にした問題です。