- 高校生Webキャンパス
- 学びの特長
- 学部独自科目
- 理学部
- 松岡甫さん


2019.12.17
数学の硬いイメージが一変した
理学部 2年生松岡甫さん
応用数理入門:これまで学んできた数学を駆使して、身の回りの現象に対して数理を用いて考えます。そうして現象の仕組みを数理的に理解し、問題解決を計る能力を養います。また、実際問題への応用能力を持つことを目指します。理工学部 開講科目。
※松岡 甫さんは 理学部 (2021年4月開設)の前身である、理工学部(募集停止)所属です。

日常生活と密接に関係する数学
この授業では、数理モデリングとその解法、ゲーム理論の基礎、社会活動解析に用いられるゲーム理論の例、進化ゲーム、一般に活用されているゲーム理論というテーマごとに、毎回、演習問題が出され、自力で考え、解けるようになることを目指します。
これまで数学と日常生活の関係はあまりイメージできませんでした。この授業を通じて、日常で出くわすシチュエーションの多くは、数学で解決できることがわかりました。

様々な事例から学ぶ
ナッシュ均衡(※)を学んだ時は、「囚人のジレンマ」と呼ばれる状況を例にしました。これは、2名の犯罪者を集め、1人ずつ取り調べを行うものです。条件として、「ともに黙秘すれば互いに懲役1年」「1名が自白、もう一名が黙秘であれば、自白側が懲役0年、黙秘側が懲役10年」「ともに自白すれば互いに懲役7年」ということが決まっています。犯罪者にとってリスクが少なく、得をする選択を考えます。
この場合、相手を犠牲にすれば自分には無罪が与えられるので、おそらく犯罪者は自白を選びます。しかし、2名とも自白を選ぶことになり、互いに懲役は7年になります。この場合は、黙秘を選択することが最善といえます。
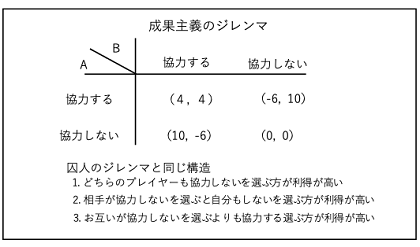
普段の生活でも、「どの選択が最善なのか」と考えることは多々あります。これまではその時に気分や過去の経験で判断していましたが、この授業で得た知識を活用して、論理的に考えられるようになりました。
※ゲームの理論において、互いに非協力的な戦略を取るプレーヤーが、自らの利得をもっとも大きくしようとする場合に実現する均衡状態。数学者J=ナッシュが提唱。

数学は役に立つ
日常のふとした瞬間に数学を使って考えることができた時は、「学んでいることが生かせた」と喜びを感じています。この授業を履修するまでは、「数学=固い」と思っていましたが、生きるうえで本当に役に立つので、すっかりイメージが変わりました。
※理工学部は理学部、工学部、生命環境学部、建築学部に再編しました(2021年4月開設)。
詳細は
こちら
。








